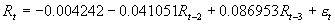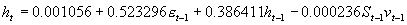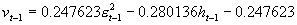对存在着杠杆效应的空头市场运用VS-GARCH模型估计的结果表明,上证综指在空头时期存在着明显的波动不对称反转现象。这一结果与Fabio and Mele(1997)对6个股票市场的分析结果相一致,说明投资者在此时期对负面的消息最为敏感,投资行为趋于理性。
中国股票市场杠杆效应研究
上海财经大学证券期货学院 李胜利
引言
在证券市场上,有价证券的波动性特征是广大投资者和基金经理们最为关注的问题。因此,关于投资风险和收益的研究一直是资产定价理论研究中的一个主要方面。经过近二十多年来的大量研究,理论界对于有价证券波动的可预测性基本上达成了一致(Bollerslev et al.,1992),而争议的焦点在于预测模型的不同选取上。例如Fama and Schwert(1977),French , Schwert, and Stambaugh (1987),Harvey(1989),Nelson(1991),Campbell and Hentschel(1992)以及Chan, Karolyi, and Stulz(1992)等分别采用不同的模型对证券市场波动性特征进行研究。
现代投资理论的一个基本观点是:在一定的时间内有价证券的收益率和风险贴水(Risk Premium)之间存在着正相关关系,但研究发现在一个较长的时间内两者关系并非如此(Glosten, Jagannathan, and Runkle,1993)。理论研究表明,正面信息和负面信息对于有价证券波动性的影响明显不同,即存在着杠杆效应(Leverage Effects)。当杠杆效应存在时,会导致波动不对称性现象:正面消息(实际报酬率高于预期报酬率)带来的正的非预期报酬会导致条件波动率变小,而负面消息(实际报酬率低于预期报酬率)带来的负的非预期报酬会导致条件波动率变大。自Black(1976)发现这一现象以来,人们对其进行了大量的研究。如Christie(1982),French , Schwert,and Stambaugh (1987),Nelson(1990),Schwert(1990),Glosten, Jagannathan, and Runkle(1993)等。1997年,Fabio and Mele又发现由于前期冲击大小的不同,杠杆效应会有不同的特征,即当前期冲击较大(实际波动率大于预期波动率)时,负冲击对未来波动的影响大于正冲击对未来波动的影响;而当前期冲击较小(实际波动率小于预期波动率)时,正冲击对未来波动的影响大于负冲击对未来波动的影响,是为非对称性反转效应(Reversions in the Asymmetric Behavior of the Volatility)。
本文使用GARCH对称模型、GJR-GARCH和VS-GARCH非对称模型,来探讨中国股票市场在全样本期、多头期、空头期以及盘整期的杠杆效应,并进一步对我国证券市场的非对称性反转效应进行研究,以揭示我国股市波动非对称性现象的规律,为管理层、机构投资者以及中小投资者判断股市的走势作一定的参考。
文献回顾
对股票市场非对称效应的研究,绝大多数是借助Engle在1982年提出的自回归条件异方差模型(Autoregressive Conditional Heteroskedasticity,ARCH)以及其所衍生出来的一系列模型进行的。金融市场中的一个常见现象,是股票或其他金融资产的变易率(Volatility)不仅随时间t变化,而且常在某一时间段中出现偏高或偏低的情况,即呈现变易率聚类(Volatility Clustering)的特点。ARCH模型充分考虑了金融资产的这一特点,给出了计算时间序列的条件方差的方法。该模型自Engle(1982)提出以来,被广泛地应用于金融市场波动性的分析,并已经被证明对资产波动性的衡量具有较强的解释能力。Bollerslev (1986)修正了ARCH模型,提出了GARCH模型,Engle, Lilien, and Robbins(1987)则进一步提出了GARCH-M模型。此后, GARCH模型不断得到扩展和改进,国外学者利用这些模型进行了大量的研究,表明GARCH模型及其扩展形式对描述金融时间序列的波动性具有非常好的效果。
Black(1976)注意到股票的波动性会因负面消息(实际报酬率低于预期报酬率)的出现而增加,并随正面消息(实际报酬率高于预期报酬率)的出现而减小,即杠杆效应。Christie(1982)提出的经济解释是:负面消息使得企业产生了负的超额报酬,企业价值降低,公司的权益资本相对于债务资本的比值下降,使其财务杠杆比率提高,投资者持有股票的风险上升,从而使其投资风险增大,导致了其股票价格报酬率的波动性增大。相反,正面消息所带来的正的超额报酬使企业价值增加、财务杠杆比率降低,投资风险和股价收益率的波动性随之减少。
Nelson(1991)采用具有非对称性的EGARCH模型来分析不同的消息对股票波动性的影响,验证了杠杆效应的存在。Glosten, Jagannathan, and Runkle(1993)在GARCH-M模型中加入季节项(Seasonal Patterns)来区分正、负冲击对股价波动的不同影响(称之为GJR-GARCH模型),并验证比较了不同的GARCH模型,证明该模型对杠杆效应的刻画具有良好效果。Engle and Ng(1993)利用日经指数1980-1988年的日交易数据,对其使用不同的GARCH模型,并设计了三个诊断非对称现象的统计量。实证结果也表明GJR-GARCH模型具有最优的效果,而EGARCH模型虽然能够捕捉大部分的非对称波动,但却高估了条件方差的波动。
Fornari and Mele(1997)系统地研究了杠杆效应,并采用6个国家的股票市场数据使用不同的模型进行实证分析,结果显示其提出的VS-GARCH模型可以刻画不对称反转效应,并且要优于GJR-GARCH模型。
近年来,国内学者对我国股票市场的波动特征进行了初步研究。如徐龙炳和陆蓉(1999)的研究表明,中国股票市场波动呈现非线性,具有状态持续性特征。徐龙炳(2001)进一步应用稳态分布理论来研究中国股票市场股票收益的特性,结果表明,中国股票市场股票收益构成的时间序列呈现狭峰、厚尾,具有稳态特征。岳朝龙(2001)分别利用GARCH模型、IGARCH模型、GARCH-M模型及EGARCH模型分析了上证综指1997年9月23日~1999年12月30日收益率的波动特征,发现我国股市的收益率具有条件异方差性。
研究方法
一、对称的GARCH模型
ARCH模型的一个最大优点在于其克服了传统时间序列模型将残差项的方差固定为不变的假定,更好地刻画了残差项的异方差特征,即条件方差随着时间的变化而变化。因此,在其基础上发展起来的ARCH族系列模型,被广泛地应用在金融市场的分析中。下面我们对其模型分别予以介绍。
1.GARCH(p,q)模型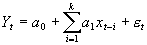 ;
; 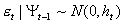 ;
; 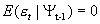
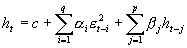
其中, 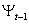 为t-1时期的信息集,
为t-1时期的信息集,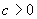 ,
, 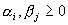 ,
, 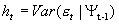 ,即条件方差。
,即条件方差。
GARCH模型在ARCH模型中加入了条件异方差的异动平均项,更好地刻画了收益率序列残差项的异方差性,若所有的β项都等于0,则其简化为ARCH(q)模型。
2.GARCH-M模型(GARCH in Mean Model)
ARCH、GARCH模型主要描述回归模型的干扰项的条件方差,一般与 的条件期望无关。但在研究中人们发现,条件方差的变化往往直接影响条件期望的值。Engle, Lilien and Robbins(1987)对其作了进一步的推广,将条件期望和条件方差都加入了回归模型之中,是为GARCH-M模型。假定其他条件不变,GARCH-M模型的收益率均值方程为:
在资本市场中,绝大部分投资者都是风险厌恶者,其投资偏好决定了其对于风险较大的金融资产要求更高的风险贴水。GARCH-M模型将风险贴水项用条件方差来衡量,将其视为风险的增函数,即条件方差越大,投资者要求的风险贴水也就越多,从而解决了这一问题。实际上,当 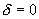 时,GARCH-M便退化为GARCH模型。
时,GARCH-M便退化为GARCH模型。
二、非对称GARCH模型
1.非对称性检验
GARCH(p,q)模型假定条件方差是过去残差平方的函数,因此,残差项的符号不会影响到条件方差,即条件方差对正的价格变化和负的价格变化的反应是对称的。然而在实证研究中发现,当坏消息出现时,即预期股票收益会下降时,收益率的波动趋向于增大;当好消息出现时,收益率的波动趋向于减小,即存在着明显的杠杆效应。条件方差是否具有不对称性,可以用Engle and Ng(1993)提出的符号偏误检验(sign bias test,SBT)、负符号偏误检验(negative sign bias test,NSBT)以及正符号偏误检验(positive sign bias test,PSBT)来检验。SBT、NSBT和PSBT是分别对模型中的残差项适配下列三个回归式后对系数估计值b进行t检验。
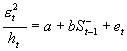 ;
;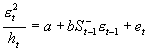 ;
; 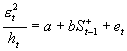
其中 , 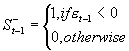 , 为残差项。
, 为残差项。
2.GJR-GARCH模型
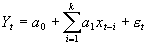 ;
; 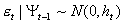 ;
; 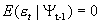
, 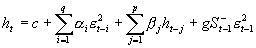 其中
其中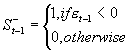
GJR-GARCH模型将前期波动的特征纳入了模型之中,当g的符号为正时,说明前期为负的冲击(坏消息),这样会导致波动幅度的增大;反之,当前期冲击为正的冲击(好消息)时,则会减缓波动的幅度。因此,GJR-GARCH模型更好地刻画了杠杆效应。
3. VS-GARCH模型(Volatility-Switching GARCH Model)
在GJR-GARCH模型中保持其他条件不变,VS- GARCH模型的残差项的回归式为:
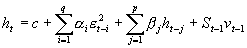
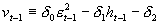
其中,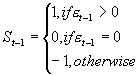 ,
,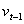 为t-1时期的非预期波动,由当期的冲击而造成。
为t-1时期的非预期波动,由当期的冲击而造成。
VS-GARCH模型除了检验波动不对称现象之外,进一步地探讨波动不对称反转效应:当前期波动较大时,负的冲击对未来波动的影响大于正的冲击所带来的影响,即负的冲击会导致本期的条件方差变大;当前期波动较小时,正的冲击对未来波动的影响大于负的冲击所带来的影响,即正的冲击会导致本期的条件方差变大。这样,由于冲击的大小不同,杠杆效应会出现完全反转的现象。
VS-GARCH模型中修正了GJR-GARCH模型没有考虑前期波动(预期的与非预期的)对当期预期波动的影响之缺点,用St-1来刻画Vt-1的符号,从而对正负不同的冲击予以甄别。
三、资料数据的收集与处理
本文采用上证综合股价指数的日交易数据之收盘价作为研究对象,分别采用上述模型来研究上海证券市场的杠杆效应和不对称反转效应。资料来源为兴汇证券分析系统,采自于上海财经大学金融实验室。样本期间自1990年12月19日至2001年12月31日,共2728组数据。所有数据处理均使用SAS软件。股价指数的日收益率用相邻两天股指对数的一阶差分来表示,其计算方法如下:
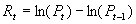
其中Pt、Pt-1分别为第t日和t-1日的股价指数。
本文为探讨股市风险分别在股市呈多头、盘整和空头时期的不同特征,分别从全样本中取了三个不同阶段的数据作为子样本,期间的选取如下:
多头期:自1999年5月19日科技股板块带动大盘上涨至2001年6月29日,共509组数据,从总体上来看,上证综指在此段时期基本上处于稳步上扬的态势。
空头期:自1993年2月16日上证综指创当时历史最高点1558.95点至1994年7月30日新的一轮行情启动,共370组数据。在本阶段,管理层相继出台了一系列规范和发展证券市场的措施,上证综指基本上呈现空头市场走势。
盘整期:自1994年11月1日至1996年9月30日,共477组数据。在此阶段,除1994年7月30日因政府出台一系 列稳定和发展的新措施(严格控制配股规模,培育机构投资者等)而造成了大盘在短时期内的不稳定外,总体上处于盘整状态。
实证结果与分析
一、各样本期收益率的描述性统计结果
首先,我们分别检验四个样本时期的描述性统计量,其结果列示在表1之中。从表1的统计结果可以看出,上证综指在多头期的平均收益率明显高于其他三个时期,而空头期的平均报酬率最低且为负值。四组数据的标准差反映出上海股市在空头期的波动性更大,而多头期的波动性最小。表1中偏度的数据全部为正值,全样本期和盘整期数值较大,反映出这两个样本期收益率数据的分布呈现明显的右偏,而其他两个样本期的分布近似对称。从峰度的数据可以看出,四个样本期收益率的分布均呈现明显的厚尾特征,并且在平均值处的波峰很尖。J-B正态检验的结果证实了股票指数每日报酬的分布不是正态分布,这与传统研究的结果相一致,即中国股票市场股票收益构成的时间序列呈现狭峰、厚尾的非正态特征(徐龙炳1999、2001等)。
表1 各样本期上证综指日收益率的描述性统计结果
|
统计量 |
全样本期 |
多头期 |
空头期 |
盘整期 |
|
Mean |
0.001191 |
0.001451 |
-0.004126 |
0.000607 |
|
Median |
0.001148 |
0.001594 |
-0.004949 |
-0.000451 |
|
Maximum |
0.719152 |
0.086650 |
0.152170 |
0.269935 |
|
Minimum |
-0.179047 |
-0.079199 |
-0.140141 |
-0.179047 |
|
Std.Dev. |
0.030861 |
0.015122 |
0.033138 |
0.027052 |
|
Skewness |
5.751560 |
0.405628 |
0.330445 |
1.801554 |
|
Kurtosis |
125.1989 |
7.992481 |
6.738122 |
27.70951 |
|
J-B |
1633913 |
542.5729 |
221.1593 |
12418.88 |
|
Probability |
0.000000 |
0.000000 |
0.000000 |
0.000000 |
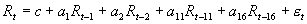
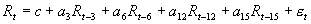
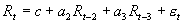
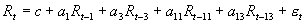
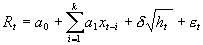
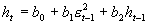
|
|
全样本期 |
多头期 |
空头期 |
盘整期 |
|
SBT |
-0.979648 (0.0274) |
-0.620103 (0.0355) |
-1.514296 (0.0308) |
-1.358743 (0.0749) |
|
NSBT |
1.96175 (0.0731) |
2.6662344 (0.0080) |
-0.264617 (0.0915) |
0.904025 (0.0665) |
|
PSBT |
0.07175 (0.0428) |
-0.215041 (0.0298) |
-0.395326 (0.0928) |
0.848755 (0.0365) |