对我国国债风险收益率的回归分析表明，国债成交量、涨幅、前一天的国债风险收益率、居民消费价格指数、央行基准利率、股指收益增长率对国债风险收益率波动过程具有较为显著的影响。

国债市场风险收益波动模式实证研究

厦门大学管理学院   吴泽福   吴世农

研究背景和文献回顾
国债市场风险收益波动模式问题是金融市场利率期限结构理论的重要组成部分，旨在研究不同期限的利率随时间的变动规律和主要的影响因素。当代关于利率的期限结构问题的主流学派，一是无偏预期理论学派，其认为零息票利率是相应期限即期利率的几何平均，而远期利率是市场对未来无风险短期利率的预期，当市场预期短期利率上升时，期限长的零息票利率高于期限短的零息票利率，收益曲线呈上扬走势，反之亦然；二是流动性偏好学派，其认为投资者在投资决策时都偏好于流动性比较强的证券，所以长期利率必须含有流动性补偿，从而高于短期利率，因此收益曲线呈上扬趋势；三是市场分割学派，其认为人们投资具有强烈的期限偏好，因此各种不同期限的债券之间不能相互替代；四是优先置产学派，其主要观点是长期利率是市场对未来短期利率预期的几何平均加上期限补偿，不同期限的债券可以互相替代，但人们又有一定的期限偏好和流动性偏好, 这一理论能较好地解释不同期限的利率具有相同走势的现象。
近20年来，国际上众多经济学家对利率的期限结构进行了广泛的研究，采用了连续时间模型和离散时间模型研究利率的随机特征。柯克斯、英杰绍尔、罗斯首先建立“平均回复模型”，对投资者偏好和经济中的可预测性变动进行假设，认为短期即期利率的运行遵循一个“平均—回复过程”。布里南和舒瓦茨(1979)建立了“两因素模型”，在单因素模型的基础上提出了短期利率在向长期利率回归的过程中，遵循一个几乎是完全无规则的单独随机过程，这比“单因素”模型有更多不同类型的期限结构的迁移。里特南、萧恩克曼、韦斯(1998)在《变动性和收益率曲线》和《影响债券收益的普遍因素》论文中建立“三因素模型”，其第三因素通常是指对变动性的测度，即与短期和长期利率类似，变动性也被允许符合一个随机过程，在这个过程中，它趋向于任意回复到变动的正常水平，但在任意时刻可以偏离这个水平。布莱克、德曼(1990)开发了单因素期限结构的离散时间模型，假设利率的变动仅由短期名义利率或时间利率的变动引起，并采用了“二项树”工具研究在离散的时间段开始或结束时利率如何在观测点之间波动，这对于现金流在某种方式上依赖于未来期限结构的有价证券的经济价值评价上是很有用的特征。
在我国，对利率期限结构的研究仍处于起步阶段，为了揭示我国国债市场风险收益率的系统波动模式及其生成机制，本文采用逐步回归分析法和时间序列分析法，运用高频数据(High Frequent Data)对我国上海国债市场风险收益日内和日间的波动模式和主要影响因素进行了实证分析，从新的视角揭示了我国国债市场利率的期限结构变动规律。

研究设计和实证方法
一、数据和样本的选择
本文研究样本为上海证券交易所上市交易 的国债逐日和每5分钟的历史行情数据，每条历史行情数据记录国债的代码、日期、成交量、成交金额四种成交价格。样本期间为2000年1月1日至2002年2月28日止。文中使用的宏观经济指标数据来源于中国统计局每月25日发布的宏观经济指标月报。无风险收益率采用期限为3个月的短期国债利率替代。
二、研究方法
本文对上海证券交易所上市交易国债品种进行短期、中期和长期分类，研究我国国债市场不同到期期限的国债品种风险收益的特征、变动趋势和主要影响因素，采用的研究方法主要包括如下几个方面：
1.采用直方图统计描述日内国债风险收益的变动特征。以5分钟为基本时段将每日国债交易时间划分为48个观测值，选取每个时段末的国债交易价格计算每个时段国债风险收益率。对于超过10分钟无交易的时段，采用“内部插值法”填补数据空缺。每个时段国债风险收益率的计算公式为：
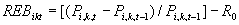                        (1)
其中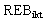： 为第i只国债第k日的第t个5分钟时段的风险收益率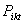；  为第i只国债第k日的第t个5分钟时段的交易价格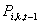， 第i只国债第k日的第t-1个5分钟时段的交易价格， 第k日市场无风险资产收益率。
2.使用协方差(公式略)估计国债风险收益率与国债交易量、涨幅、通货膨胀率、央行基准利率、汇率、居民消费价格指数增长率、上证A股指数增长率等经济指标的相关程度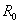，为进一步研究和确定国债风险收益率的影响因素奠定基础。
3.采用逐步回归分析法检验央行基准利率、汇率、成交量、涨幅、居民消费价格指数增长率、上证A股指数收益率等宏观经济指标对国债风险收益率是否具有显著的影响。筛选了加入后使检验统计量F值的显著性小于并等于0.05的变量, 删除了加入后使F值的显著性大于并等于0.10的变量。用Jarque Beta统计量检验逐步回归模型的残差是否服从正态分布，用Box-Pierce-LjungQ统计量 检验逐步回归模型的残差是否为白噪音，用GARCH回归分析法消除使用时间序列数据估计回归模型时通常存在的自回归条件异方差(Auto-Regressive Condotional Heteroscedasticity)问题。

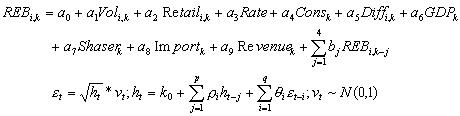 （2）
其中：REBi,k为第i只国债第k日的风险收益率，Ratek为第k日的央行基准利率，Voli,k为第i只国债第k日的成交量，Cons为居民社会消费指数增长率，Shaserk为上证A股指数第k日的增长率或收益率, Soc为社会消费品价格指数增长率，Retail为零售品价格指数增长率，Rev为居民人均收入增长率，Diffi,k是第i只国债第k日的涨幅；GDP是国民生产总值，Import是进出口总额的增长率；Retail是商品零售价格指数；Revenue是城镇居民家庭可支配收入增长速度； 分别是GARCH模型中残差的滞后期。通过上述的回归模型分析来确定影响国债风险收益率的主要因素。
实证结果和分析
通过对国债风险收益率的日内与日间波动模式的特征分析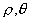，可以了解我国国债市场利率期限结构的形成机制。为此，我们应用上述的统计方法对采集的样本数据进行分析得出如下实证结果。
一、日内国债风险收益率的波动模式分析
比较样本期间507个正常交易日，分别以5分钟为时段的国债风险收益率和绝对风险收益率的时间序列直方图后，可以看出，以5分钟为时段的国债风险收益率时间序列直方图并没有显示出以5分钟为时段的国债风险收益率具有系统性的波动特征，而是沿着平均风险收益率上下波动。但以5分钟为时段的国债绝对风险收益率的时间序列直方图却呈现出在开盘后的前几个单位时段的绝对风险收益率较高，而在日中的单位时段的绝对风险收益率较低，在接近收盘时的几个单位时段的绝对风险收益率又呈回升走势，因而呈现日内“U”型波动模式，但这与股票市场的日内强“U”型波动模式相比，显得非常微弱，而这种日内弱“U”型波动模式导致了日间国债绝对风险回报的自相关波动模式。
二、日间国债的风险收益率的波动特征分析
从上海证券交易所上市交易的国债2000年1月4日至2002年2月28日共507个交易日的风险收益率的数据波动分析图(略)可以看出，日收益率序列中没有明显的趋势部分，但在日收益序列中表现出波动集束的现象，即在一些时段内收益波动较为剧烈，在另一些时段内收益波动相对平稳。
为了说明国债日收益率的其他性质，在表1中列出日收益率数据的一些基本统计值，根据这些统计值可得出如下结果：
1.从均值和方差看, 上证国债日平均风险收益率较低, 风险也较低。但1999年以后发行的国债的日风险收益率明显较以前发行的国债高，风险也较以前发行的国债低，呈现出市场水平的阶段性特征，这种现象的产生与1999年央行降低各项存款利息以及我国国债市场机制建设的日趋完善有关。
表1   上证国债日收益率的基本统计描述表

 

说明： Q是标准化后残差的 Ljung-Box Q统计量，Jarque Beta 是正态检验统计量，**代表显著性水平为0.05，96国债（7）代表1996年发行的期限为7年的国债，其余类推。
2.从偏度和峰度看，上证国债日平均风险收益率的分布具有较严重向左的偏斜度和宽尾的特征，这表明我国国债投资行为具有同向性的现象，即市场具有收益时，更多的人会有收益；市场亏损时，更多的人会亏损，但这种现象对1999年以后发行的国债有明显的逆转。
3.从Jarque Beta统计值看，各只国债的检验值均为显著，这表明它们的日风险收益率均不符合正态分布。这个结果与偏度和峰度值是一致。
4.Q(5)、Q(10)、Q(30)分别是Ljung-Box修正统计量，在95％的水平下，Q(30)拒绝30期收益不是序列相关的假设，即在期限类型的风险收益序列中存在序列相关。
三、国债风险收益率波动的影响因素分析
Li，Engle(1998)和Bollerslev(2000)分别研究发现消费价格指数、物价指数、就业形式报告等宏观经济信息的发布对美国国债市场的风险收益率具有显著的影响。Fleming和Remolona(1997)分析了美国国债一年内的日内风险收益数据，发现国债价格、成交量的最大变动是来自宏观经济信息，而且影响力最大的是消费价格指数和就业形势报告两种经济信息。本文根据上述相关性分析认为，选取了居民消费价格指数增长率、上证A股指数收益率、GDP增长速度、社会消费品零售总额增长速度、商品零售价格指数、城镇居民家庭可支配收入增长速度、进出口总额增长速度、消费者信心指数增长率、汇率、通货膨胀率等宏观经济指标，分析它们与我国国债日风险收益率的相关程度。分析计算对国债风险收益率影响程度较为显著的因素的相关系数(过程略)，可以看出，我国国债日风险收益率与经济景气指数相关度最高(0.3525)，即当社会经济景气指数高时国债日风险收益率也高，反之亦然；其次是与居民消费价格指数增长率相关度较大(－0.368)，即当居民消费价格指数增长时国债日风险收益率呈减少趋势；再次是与社会消费品零售总额增长速度的相关度(－0.217)，即当社会消费品零售总额增长时国债日风险收益率呈减少趋势，与上证A股指数收益率也呈弱负向相关，这与债券市场的“翘翘板”作用是一致的；国债日风险收益率与城镇居民家庭可支配收的增长速度指标呈较弱的正向相关。另外，央行基准利率、汇率对国债日风险收益率也有一定的影响。
根据表2逐步回归模型的估计结果可见， 国债成交量、涨幅、前一期的国债风险收益率、居民消费价格指数、央行基准利率水平、上证A股指数收益增长率对我国国债日风险收益率有显著的影响。对各期限类型国债波动模式中的b1估计值在整个样本期内均是显著的，这表明国债的风险收益率与上一天风险收益率存在正向序列相关，但总体而言，这种相关性比较弱。各期限类型国债波动模式中的a3值表明，国债风险收益率与同期的居民消费价格指数呈显著的负相关关系，即当居民消费价格指数上升时，国债风险收益率下降，反之亦然。从估计参数a5可以看出，国债风险收益率水平与同期中央银行基准利率水平显著负向相关，而且从1999年6月央行再次大幅降息后发行的国债的风险利率水平与同期央行基准利率水平相关程度更大，与债券本身日成交量呈弱反向相关。Bollerslev et al.(1992)研究得出美国国债风险收益的波动性具有明显的自相关性，而且波动的持续性较强，随时间的衰减程度缓慢。
表2        逐步回归模型的估计结果

	96国债(10)	96国债(7)	97国债(10)	99国债(8)	99国债(10)	00国债(7)
a (*E-10)	-0.128 (-5.363)***	-0.128 (-5.963)***	-0.096 (-3.619)**	-0.057 (-2.719)**	-0.057 (-2.519)**	-0.114 (-4.417)**
b(*E-2)	0.056 (-2.658)**	0.056 (-2.958)**	0.061 (-4.526)*	0.063 (-2.982)*	0.063 (-2.582)*	0.181 (-8.218)***
a(*E-4)	-0.131 (-2.238)***	-0.131 (-2.638)***	-0.090 (-3.698)*	-0.043 (-2.982)**	-0.043 (-2.942)**	-1.91 (-2.238)***
a(*E-2)	0.0335 (2.046)**	0.0335 (2.016)**	0.038 (2.385)**	0.043 (2.046)**	0.043 (2.096)**	0.145 (7.245)***
a	-0.010 (-2.139)**	-0.010 (-5.362)**	-0.0065 (-2.365)*	-0.045 (-2.139)**	-0.045 (-3.256)**	-0.035 (-3.139)**
k(*E-05)	1.67 (2.843)*	1.66 (3.332)*	1.71 (2.099)*	1.72 (2.321)*	1.77 (4.231)*	1.61 (2.313)*
	0.152 (1.477)*	0.151 (1.565)*	0.152 (1.875)*	0.152 (2.445)*	0.150 (3.485)*	0.152 (1.925)*
	0.213 (5.313)***	0.212 (5.926)***	0.210 (6.353)***	0.211 (4.654)***	0.213(7.753)***	0.212(8.112)***
Durbin-Watson	2.000	1.981	2.258	1.981	1.981	1.990
F值	5.003	5.123	4.012	5.698	6.343	7.325
F值的显著性水平	0.000	0.000	0.000	0.000	0.000	0.000

Jones et al.(1998)研究认为美国国债波动过程符合单变量GARCH过程。而本文对式(2)的回归结果表明，我国国债的风险收益率的波动也遵循一个GARCH(1,1)过程，即式(2)回归模式估计结果的残差的标准差是由前一期的标准差和前一期误差项决定的，而对各期限类型的国债风险收益率的波动模式中的ARCH、GARCH系数均显著为0.1491和0.2125左右，这表明我国国债日收益率序列也具有一定的波动持续度,而且与利率期限结构基本无关。从GARCH过程的k0值看，各期限类型国债的恒波动因子不同，这说明各期限类型国债的内在波动风险是不同。

结论与建议
本文从日内和日间两个角度入手，运用直方图等直观的统计描述方法对我国国债市场收益率的波动模式进行较全面的研究，并利用逐步回归和时间序列分析方法，研究波动过程的主要影响因素。实证研究中得出的主要结论有：
1.我国国债市场经过近10年的发展，市场特征发生了阶段性的变化，表现为在市场风险大幅降低的同时，市场平均收益水平提高。但国债市场本身的有效性问题从本文研究中仍然找不出有效的证据。
2.我国国债风险收益率的日内波动具有较弱的“U”型模式，在每日开盘后的前几个5分钟时段的风险收益率较高，而在交易日中的5分钟时段的风险收益率较低，但在接近收盘的后几个5分钟时段的风险收益率呈上升趋势。
3.我国国债风险收益率的日间变动具有明显的宽尾和波动集簇的特征，其波动的持续度较大，也即波动程度的衰减过程较慢，而且与利率的期限结构无关，这表明国债投资具有一定的“羊群效应”，即国债投资行为是一个群体上升与下扬的连续过程。
4.通过逐步回归法和GARCH回归模型的参数估计后，发现我国国债风险收益率的回归模型中，国债成交量、涨幅、前一天的国债风险收益率、居民消费价格指数、央行基准利率、股指收益增长率对国债风险收益率波动过程具有较为显著的影响，而且国债日间风险收益率序列存在自相关，特别是当期风险收益与前3天的风险收益存在不同程度正相关，但其相关程度较弱。
据此，我们提出两点建议：
一是进一步完善我国国债市场制度建设。当前深沪国债市场与银行间国债市场相对分割对国债市场流通效率必然造成一定的影响，笔者认为应以实施银行柜台债券交易制度和国债做市商制度以基础，探索交易所国债市场与银行间国债市场的整合途径，大力推进我国国债市场效率的规范化建设，逐步形成以国债市场利率为市场基础利率的利率构成体系。
二是在扩大国债交易流通量的同时增加可交易国债品种。1999年国家发行的9000亿国债中只有一部分可以流通，而其中大部分可流通国债只在银行间国债市场流通，在上海证券交易所流通的国债只有不到1000亿元，约为当年GDP的1/80。另一方面，我国国债交易品种较少，2002年底上海国债市场中流通的国债现券品种不上十种，与美国相比差距很大。这些问题在当前央行基准利率不断下调，大型投资公司的迅速涌现，个人投资者缺乏有效投资途径的情况下，必然要求我国的国债交易市场尽快增加可供多元投资者介入的国债投资品种，并扩大国债市场交易的流通总量，避免造成市场需求的同向性和市场的大幅波动。 ■