证券市场作为金融市场的重要组成部分,其剧烈的波动性和巨大的交易量使其成为风险管理的主体。如何对证券风险进行有效的计量和管理,是市场各方面对的重要课题。作为目前发达证券市场上测量市场风险的主流方法,实证研究表明,Risk Metrics模型的VaR值计算方法对我国证券市场上的风险管理有较好的效果。
长城证券 杜海涛
引言
近年来,随着世界金融市场的日趋规范、壮大,各金融机构之间的竞争也发生了根本性的变化,即从过去的资源掠夺转变为内部管理与创新方面的竞争,从而导致了各金融机构的经营管理发生了深刻的变化,金融风险管理成为现代金融机构管理的基础和核心。尤其是我国即将加入WTO,国内金融机构面对即将到来的全球金融一体化的挑战,就更突出了金融风险管理的重要性。证券市场作为金融市场的重要组成部分,剧烈的波动性和巨大的交易量使其当之无愧地成为金融风险管理的主体。从巴林银行的倒闭到美国长期资本管理公司的破产,都说明了在证券投资中加强风险控制的重要性和必要性。
传统的ALM(Asset-Liability Management,资产负债管理)过于依赖报表分析,缺乏时效性;利用方差及β系数来衡量风险过于抽象、不直观,且反映的只是市场(或资产)的波动幅度;而CAPM(资产定价模型)又无法揉合金融衍生品种。在上述传统的几种方法都无法准确定义和度量金融风险时,G30集团在研究衍生品种的基础上,于1993年发表了题为《衍生产品的实践和规则》的报告,提出了度量市场风险的VaR(Value at Risk:风险价值)已成为目前金融界测量市场风险的主流方法,稍后由J.P. Morgan推出的用于计算VaR的Risk Metrics风险控制模型更是被众多金融机构广泛采用。目前国外一些大型金融机构已将其所持资产的VaR风险值作为其定期公布的会计报表的一项重要内容加以列示。
VaR风险控制模型简介
G30、J.P. Morgan提出的VaR风险控制模型在1995年世界银行巴塞尔委员会上被认可采纳之后广泛应用于国外金融机构的风险管理中。某种资产或投资组合的VaR是如下定义的:在一段时间内,该项资产的价值损失(可以是绝对值,也可以是相对值)不超过VaR的概率必须等于预先确定的值(即统计学上的置信度)。用公式表示为:
P(X<VaR)=α,其中P为概率(Probability),X为某项资产的损失额,VaR为风险价值即可能的损失上限,α为给定的概率即置信度。
例如,对某项5亿元的投资,在考察其一段时期的或有损失时,根据95%的置信度求得VaR为2500万元(假设)。则依据上述定义可得:我们有95%的把握判断该项投资在下一个交易日内的损失在2500万元以内,亦或损失超过2500万元的概率仅为5%,平均20个交易日才可能出现一次这种情况。另外α值(置信度)可根据不同的投资者对风险的偏好程度和承受能力来确定。
目前已开发出来的计算VaR值的风险管理软件很多,如J.P. Morgan的Risk Metrics系统、金融工程协会(FEA)开发的VaRdelta系统等。其中J.P. Morgan的Risk Metrics系统是一种开发较早且应用最为广泛的VaR风险控制模型。该模型通常假设如下:
1.市场有效性假设(有效性定义:有关证券的各种信息均反映在其价格中);
2.市场的波动是随机的,不存在自相关性。
在此假设下即可得到某证券的日收益率Xt=ln(Pt/Pt-1) (此处利用每日的对数收益率来近似实际的收益率(Pt-Pt-1)/Pt-1,其中Pt为t日的收盘价格)服从均值为0的正态分布即Xt~N(0,σ),然后再根据正态分布的特性计算出给定置信度下的日收益率。
由于我国证券市场起步较晚,市场尚需规范,不能完全满足强有效性的假设,另外,政府的干预和机构的坐庄行为也使得波动具有自相关性,故我国证券市场日收益率的波动不能完全满足正态性。在利用Risk Metrics模型时,只能将其近似为正态处理。事实上完全满足上述条件的市场是不存在的,其只是为利用数学模型计算而设计的一种理论上的假设。
VaR模型在证券市场中的应用
一、市场指数的风险度量
就目前我国两个交易所制定的市场指数而言,其实质上所代表的是一种资产组合,综合指数的风险(即系统风险)是无法消除的。如何准确地度量市场风险,更好地进行市场运作,是投资者们广泛关注的问题。同时对于股指期货而言,综合指数又是该衍生品种的载体,要研究高风险的指数期货就必须对其指数载体进行研究。下面我们就投资者广泛关注的上证综合指数、深证成分指数、深证综合指数来分别计算其VaR值。
1. 正态性检验
首先根据2000年1月4日至2000年6月2日期间共94个交易日的日收益率做分布直方图,由于深沪两市场具有高度相关性,此处仅以上证综合指数为例计算。结果如图1。
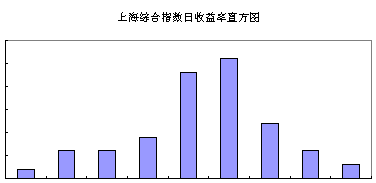
从图1可以看出上证综合指数日收益率分布表现出较强的正态特征:众数附近十分集中,尾部细小。分析表明,深市指数也有相同的特征。
下面利用数理统计的方法对2000年4月3日至6月2日期间上述3种指数的日收益率的分布情况进行正态性检验,检验结果如下:
W(深证综指)=0.972445
W(深证成指)=0.978764
W(上证综指)=0.970279
W为正态假设检验统计量,当样本容量为40时取α =0.05(表示我们犯错误的概率仅为 α=0.05),此时W0.05 =0.94,只有当W <W0.05 时我们拒绝原假设。从我们的检验结果来看,我们无法拒绝三种指数的日收益率服从正态分布的假设。
有关这三种指数日收益率的相关统计量见表1。
表1 三种指数日收益率统计量
|
|
深圳综合 |
深圳成分 |
上证综合 |
|
均值( |
0.001318 |
0.001061 |
0.001561 |
|
标准差( |
0.013363 |
0.012582 |
0.012391 |
通过上面的分析,我们可以得出三种指数的日收益率基本上服从N(μ,σ) ,由于三种指数的平均日收益率非常接近零值,故可近似为N(0,σ)。
2. VaR的计算
由于正态分布的特点,集中在均值附近左右各1.65σ区间范围内的概率为0.90,用公式表示为:P(μ-1.65σ<X<μ+1.65σ)=0.90,再根据正态分布的对称性可知P(X<μ-1.65σ )=P(X>μ+1.65σ)=0.05;则有P(X>μ-1.65σ)=0.95。根据上面的计算结果可知在95%的置信度情况下:
VaR值=T日的收盘价×1.65σ。
取2000年4月3日至2000年6月2日的数据,然后根据上面的公式可以计算出深证综指、深证成指、上证综指3种指数在2000年6月2日的VaR值分别为:
深证综合指数VaR=591.34×1.65 ×0.013363=13.04
深证成份指数VaR=4728.88×1.65 ×0.012582=98.17
上证综合指数VaR=1916.25×1.65 ×0.012391=39.17
其现实意义为:根据该模型可以有95%的把握判断指数在下一交易日即6月5日的收盘价不会低于T日收盘价-当日的VaR值;
即深证综合指数不会低于:591.34-13.04=578.30
深证成份指数不会低于:4728.88-98.17=4630.71
上证综合指数不会低于:1916.25-39.17=1877.08。
3. 可靠性检验
现在来检验该模型的可靠性。根据3种指数的VaR来预测下一个交易日的指数变动下限,并比较该下限和实际收盘价,看预测的结果与我们期望值之间的差别。图2、图3、图4是3个指数于2000年4月3日至6月2日的实际走势与利用VaR预期下限的拟合图形。
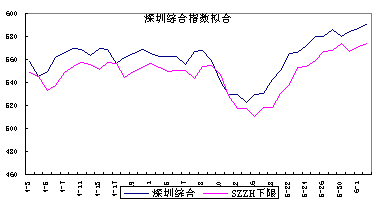
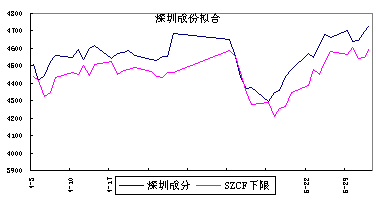
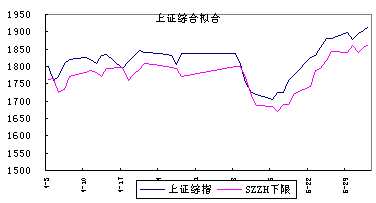
现将样本区间内实际收盘指数低于预测下限的天数与95%置信度情况下的可能出现的期望天数作一统计对比,结果见表2。
表2 模型期望结果与实际结果的比较
|
|
深圳综合 |
深圳成分 |
上证综合 |
|
实际情况 |
3 |
3 |
3 |
|
期望情况 |
2 |
2 |
2 |
通过上面的计算我们可以发现应用VaR模型进行指数风险控制拟合结果较好。至于三种指数均有3个交易日超过预测下限,这主要是由于考察期间适逢台湾政权更迭及美众院审议表决予华PNTR的议案,市场波动较大所致。
二、单个证券的风险度量
单个证券的风险度量是投资者最关心的问题之一。以某只股票为例,能否准确掌握股票价格的变化,选择买卖时机,是投资者制胜的法宝。对于单个股票价格的VaR计算雷同于指数的VaR计算方法。只是由于股票会有分红派息、送股、配股的问题,这就需要对股票价格进行调整,使得前后价格具有可比性。通常我们采用向前调整的办法。具体做法如下:
送股:计算考察期内每日的收盘市值除以当前的总股本,即可得到向前调整的股票价格时间序列。
配股:计算考察期内的每日收盘市值,对于配股除权以前的股票市值需加上应配股数乘以配股价格,再除以应配后的总股本,即可得到配股除权以前的价格;除权后的价格不需变化(此法主要针对上交所配股除权办法而设计)。
派息:计算考察期内的市值,对于分红派息以前的市值需减去该期内的分红总金额后除以当日总股本即为调整后的价格。
复合分配的处理:对于当期采取多种分配方案的上市公司的股票价格进行调整时,应按各种方案除权的先后套用如上公式进行。
不失一般性,下面将按照上述做法计算江西纸业(600053)、上海梅林(600073)、清华同方(600100)及大唐电信(600198)的VaR值。
1.正态性检验
数据来源为2000年4月3日至6月2日共38个交易日的每日收盘数据。上述4只股票除上海梅林外在该考察期内均有过送配,故需依据上述方法对股票价格进行向前调整,然后对上述4只股票的日收益率进行正态性检验,结果如下:
W(上海梅林)=0.939899
W(大唐电信)=0.970828
W(江西纸业)=0.971951
W(清华同方)=0.943855
当样本容量为38时α取 =5%,此时 W0.05=0.938。从检验结果来看,我们无法拒绝上海梅林、大唐电信、江西纸业、清华同方的日收益率服从正态分布的原假设。
上述4只股票日收益率的相关统计量见表3。
表3 四只股票的日收益率统计量
|
|
上海梅林 |
大唐电信 |
江西纸业 |
清华同方 |
|
均值( |
-0.0050849 |
-0.0030806 |
0.0007979 |
0.0009952 |
|
标准差( |
0.0340609 |
0.0206919 |
0.0307398 |
0.0225482 |
从上面的结果可以看出上述4只股票的日收益率近似服从N(0,σ)。
2. VaR的计算
下面我们来计算上述4只股票6月2日的95%置信度情况下的VaR值,见表4。
表4 4只股票的有关VaR值计算结果
|
|
上海梅林 |
大唐电信 |
江西纸业 |
清华同方 |
|
VaR值 |
1.07 |
1.11 |
0.59 |
1.71 |
|
预期低价 |
17.93 |
31.34 |
11.13 |
44.29 |
|
预期跌幅 |
-5.62% |
-3.41% |
-5.07% |
-3.72% |
|
6.5实际最低价格 |
18.60 |
32.20 |
11.30 |
45.38 |
|
6.5实际收盘价格 |
19.55 |
32.60 |
11.31 |
46.70 |
根据上述计算结果,我们有95%的把握判断下一个交易日(6月5日)清华同方的价格不低于44.29(跌幅不超过3.72%),其他股票亦然。上表反映了上述4只股票在6月5日的实际收盘价格及最低价格均未超出我们的预期下限。
3. 拟合结果检验
现将考察的38个交易日内的实际收盘指数低于预测下限的天数与95%置信度情况下的可能出现的期望天数做一统计对比,结果见表5。
表5 模型期望结果与实际结果的比较
|
|
上海梅林 |
大唐电信 |
江西纸业 |
清华同方 |
|
实际情况 |
1 |
2 |
2 |
2 |
|
期望情况 |
1.9 |
1.9 |
1.9 |
1.9 |
从表5我们也可看到,拟合效果是非常好的。
另外关于债券的风险度量,也雷同于单个股票的算法,只是对于债券而言直接考察的并非其价格,而是每日的收益率,计算出每日收益率的VaR后,再根据每日收益率与股票价格的敏感性分析得出其价格的VaR。
三、其他金融品种的风险度量
由于期货交易价格变动很大,若因保证金不足而被强行平仓可能会带来很大的损失;若预留保证金过多则要承担资金成本,故如何控制期货保证金的问题也是业内人士普遍关注的焦点问题之一。我们在此将每日需要的保证金视为股票价格或指数,按如上方法即可计算出有关期货保证金的在某一时点的VaR值。
另外,VaR模型在金融衍生品种的风险度量方面也起着重要的作用,鉴于数据的原因及我国目前证券市场的现状,此处将不再具体计算。但衍生品种的VaR计算与上述的方法基本相同。
VaR模型在证券经营机构中的应用
通过VaR模型对各种证券进行风险度量,然后判断或有损失,从而进行风险管理、组合调整,这是证券经营机构利用VaR模型的整体思路。下面以证券投资基金为例来说明VaR模型的具体应用。
一、计算证券投资基金净值的VaR
我们以基金开元(4688)、基金普惠(4689)、基金金泰(500001)、基金安信(500003)、基金裕阳(500006)为分析对象,取2000年1月7日至6月2日19个交易周的单位净资产值为样本进行分析。
1.正态性检验
对上述19个样本点进行正态性检验结果如下:
W(基金开元)=0.95258
W(基金普惠)=0.96109
W(基金金泰)=0.94386
W(基金安信)=0.972156
W(基金裕阳)=0.963995
当样本容量为19时α取 =5%,此时W0.05=0.901。从检验结果看,我们无法拒绝基金开元、基金普惠、基金金泰、基金安信和基金裕阳的正态性假设。有关的统计量见表6。
表6 5只基金的相关统计量
|
|
基金开元 |
基金普惠 |
基金金泰 |
基金安信 |
基金裕阳 |
|
均值( |
0.015648 |
0.013788 |
0.015559 |
0.017274 |
0.014334 |
|
标准差( |
0.045623 |
0.03748 |
0.035623 |
0.037033 |
0.036559 |
2.VaR值的计算
计算2000年6月2日的95%置信度情况下的VaR值,结果见表7。
表7 5只基金的有关VaR值计算结果
|
|
基金开元 |
基金普惠 |
基金金泰 |
基金安信 |
基金裕阳 |
|
VaR值 |
0.1459 |
0.1085 |
0.1021 |
0.1327 |
0.1184 |
|
预期低值 |
1.7920 |
1.6453 |
1.6347 |
2.0383 |
1.8450 |
|
调整后预期低值 |
1.5420 |
1.4143 |
1.4677 |
1.7183 |
1.4850 |
|
预期最大跌幅 |
-7.53% |
-6.18% |
-5.88% |
-6.11% |
-6.03% |
(注:调整后的预期低值是扣除当年的分红后的预期低值)
以基金裕阳为例,我们有95%的把握判断基金裕阳下周(6月12)公布的单位净资产值的最大跌幅不会超过0.1185元或-6.03%。若基金裕阳的管理人希望下周有95%的把握保证基金的单位净资产值的跌幅不超过3%,则根据我们的预测情况,该基金的投资组合显然不能满足基金经理人的要求,此时应该对基金投资组合进行调整,剔除或降低风险大(即VaR值大)的券种的投资比例,增加风险小的券种的仓位。
对于证券公司的自营情况也可以完全套用此模式进行风险管理。
二、衡量资产管理人员的绩效
对于基金经理人或证券经营机构资产管理人员操作绩效的衡量一直是大家广泛探讨的问题。高的收入意味着要承担高额风险。如何来衡量风险与收益的平衡点,使得我们能在给定风险的情况下实现最大收益,或在给定收益的情况使得风险最低?SHARPE比值法是前期报刊媒体广泛讨论的比较各证券投资基金操作绩效的一个指标。
本文要介绍一种目前西方投资银行和基金公司广泛应用的衡量资产管理人员业绩情况的指标--RAROC(Risk Adjusted Return on Capital,可调整风险的资本收益率)。其计算方法为:
RAROC=该期的平均资本收益率÷该期的VaR值。
表8是基于前部分计算结果的基础上得出的各证券投资基金的RAROC(收益率取2000年1月1日至6月2日的净资产增长率)。
表8 5只基金管理人的RAROC比较
|
|
基金开元 |
基金普惠 |
基金金泰 |
基金安信 |
基金裕阳 |
|
VaR值 |
0.1178 |
0.0919 |
0.0880 |
0.1240 |
0.1185 |
|
收益率 |
0.4153 |
0.2982 |
0.3592 |
0.4206 |
0.3309 |
|
RAROC |
2.8467 |
2.7495 |
3.5188 |
3.1707 |
2.7938 |
|
日收益率的标准差 |
0.045623 |
0.03748 |
0.035623 |
0.037033 |
0.036559 |
通过表8我们可以看出,在承担同样的风险的情况下基金金泰的收益率最高。按RAROC指标来衡量上述5家证券投资基金的优劣情况如下:金泰>安信>开元>裕阳>普惠。
该方法也同样适合机构投资者内部各操盘人员的绩效考核。
三、配股价格的确定
一级市场随着发行方式的改变,也改变了券商的竞争策略,审核制的推行、发行价格限制的取消同时增大了承销团的风险。尤其是对于配股项目而言,配股价格定低了不利于承销商的竞争,高了又要承担包销风险。VaR模型的应用,可以很好地缓解这一矛盾。以江西纸业和大唐电信为例,我们只需计算这两只股票在某个时点的VaR值,计算出其在某个概率下可能到达的最低价格,再根据各券商对大市及个股的趋势研判,确定一个适当的折扣比率,就可以科学地确定一个股票的配股价格了。
由于从配股项目的争取到报批周期较长,故我们可以根据不同的情况制定出在各种置信度情况下(此处以95%的置信度为例)的VaR值。假设配股说明书见报前3个月就需报送材料、确定配股价格,我们分别取江西纸业在2000年1月14日以前40个交易日的数据及大唐电信在2000年2月29日以前40个交易日的数据计算其VaR值,结果见表9。
表9 2只股票的有关VaR值计算结果
|
|
江西纸业 (2000年1月14日) |
大唐电信 (2000年2月29日) | ||
|
VaR |
0.34元 |
2.68元 | ||
|
预期低点 |
8.06元 |
30.73元 | ||
|
折扣比率 |
10% |
15% |
10% |
15% |
|
折扣价格 |
7.25元 |
6.85元 |
27.66元 |
26.12元 |
|
实际配股价格 |
6.88元 |
26.00元 | ||
从表9可以看出在配股说明书见报前3个月,以95%的置信度计算出的股票价格折扣15%后所得的值基本上与实际配股价格相符。事实上,有关折扣比率的确定可根据券商能够承担的风险能力、对后市的预测、对个股的研究等综合因素加以确定。
四、其他应用
VaR模型也可用于管理证券公司客户保证金,掌握其变动规律,及时预测其变化情况;也可用于债务的组合管理。对于融资比较频繁的金融公司而言,利用VaR可以较好地控制账面现金以备偿还到期债务之用。 ■