以Black-Scholes期权定价公式刻画认股权的价值,可以方便地对可转债券价格进行标准的比较静态分析。但是,这种分解在定价实务中的应用价值并不大,甚至可以说会使人误入歧途。分析表明,二项分布模型能更为灵活地处理可转债中的各种复杂条款。
可转换公司债定价问题研究
为什么基于Black-Scholes期权定价公式对可转债的定价通常是错误的
从理论上说,可转债可以视为一个普通债券与一个认股权证,以及其他期权的叠加。具体来说,一个典型的可转债契约包含五个组成部分,即纯债券(straight bond)、认股权证(warrant)、赎回条款(callability)、回售条款(puttabilty)、转换价修正条款(refix clauses)。对于研究可转债价格特征和规律,这种分解具有明显的理论意义。譬如,以Black-Scholes期权定价公式刻画认股权的价值,可以方便地对可转债券价格进行标准的比较静态分析。但是,这种分解在定价实务中的应用价值并不大,甚至可以说会使人误入歧途。原因在于可转债中各部分是有机地结合的,每一部分独立估价常常不可行:
第一,当标的股票派发股利,或者可转换债具有提前赎回和回售条款的时候,可转债中的期权具有美式期权性质,持有者可能在到期日前转股(或回售),从而转债中的纯债券期限预先无法确定,为其定价显然是不可行的。
第二,由于可转债中蕴含的美式期权性质,不仅认股权证部分的价值不能直接套用Black-Scholes欧式买权定价公式,而且投资者是否选择提前转股与赎回条款和回售条款等相互交错,不考虑这些条款,认股权的价值估计必然是有偏差的;同时,不考虑投资者提前转股的可能性,赎回条款和回售条款的估价也是片面的。第三,如果契约包括转换价向下修正条款,可转债价值将依赖于股价路径(详见后文),而Black-Scholes定价结果只与股价初值和终值有关,股价过程的信息无法体现在定价过程和结果中,所以这项条款对可转债价值的影响也无法作出精确的评估。
只有在可转债没有赎回条款、回售条款和转换价格修正条款,有效期内标的股票不发放股利的特殊情况下,可转债价值才可以确切地表示为:
CB=SB+W (1)
其中CB为可转债价值,SB和W分别为其中纯债券和认股权的价值。
由于在存续期内没有股利发放,可转债中的认股权不会提前执行,W可以直接套用Black-Scholes欧式买权定价公式计算,而SB则由标准的收益流量现值方法估值。
二项分布定价基本模型
由于上述原因,可转债定价通常只能求数值解。在常用的数值方法中,著名的蒙特卡罗模拟方法局限于欧式期权证券定价(Hull, 1993),可以排除在外;另一方面,虽然有限差分和二项分布模型都可以处理美式期权定价问题,而且前者在做大批量期权价格计算时更显效力(Geske and Shastri, 1985),但我们认为二项分布模型能更为灵活地处理可转债中各种复杂条款。
可转换公司债券属于一种金融衍生产品,任何一种定价模型都可分为两个步骤:先模拟标的股票价格变化过程,再在此基础上推导它的当前价格。譬如,Black-Scholes定价模型假设股票价格作几何布朗运动,而(重复)二项分布定价模型假设股价在一个很小的时段上呈二项分布。
一、单期模型
二项分布定价模型也称二叉树定价模型,基本原理来自Cox, Ross and Rubinstein (1979)提出的期权定价的方法。由于可转债收益结构与买权极其相似,可以毫无困难地加以移植应用。假设时间作离散变化,并且只有一期,即可转债在时刻T=1到期,当前时刻为T=0。记发行者股票现在的市场价格为S,其未来价格只有两种可能值:上涨至uS或者下跌至dS,u>d>0(见图1)。如果无风险利率为r,则无风险收益率Rf=1+rf必然居于d和u之间:d<Rf<u,否则会出现套利机会。记可转债的转股价为x,在到期日T=1,其价值也对应两种情况。图1同时显示了可转债的可能变化值。


其中pu和pd分别是股价上涨和下跌的风险中立概率,要注意它们与实际概率无关--事实上,通过构造风险对冲组合并利用套利原理,可以推知: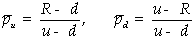
二、两期模型
如果T=2,标的股票每一期有两种可能的变动情况,且各期的涨跌幅度相同:St=uSt-1或St=dSt-1。如果目前它的价格是S,股票和可转债价格的未来变化如图2所示。
|
|
在T=1时,可转债的寿命还剩下一期,此时我们面对的问题与持有一份寿命为一期的可转债时相同。利用倒推公式(2),可得出这个二期模型中的可转债价格,即:
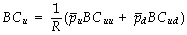
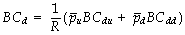
三、n期模型
显然,假设公司股票只有2种或者4种变化可能情况是极不现实的。解决这个问题的一个办法是,将可转债有效期[0,T]时段细分为均匀的n个小时段,在每一小时段上作二项分布假设,这样最终股票的可能变化就有 n+1种,这同时决定了到期日可转债的n+1种可能价值。从最后一期开始,反复利用倒推公式(2),即可一步一步地反推出可转债的当前价格。经验证明, 50~200期的模型就能获得相当精确的结果了。事实上,一个50期的模型与一个100期的模型相比较,二者的计算结果相差仅0.02%左右(Connolly, 2000)。
在无股利、无赎回条款和回售条款,同时也没有转换价格修正条款的情况下,可以直接利用风险中立概率定价原理,得到二项分布模型的显式解。二项式定价模型的优点是它能逮获股价路径信息,而极限结果却丧失了这一特性,只保持了到期日的股票终值。所以,在处理有票息、股利以及其他附加条款的可转债时,必须要在n期模型中一步一步地反复使用倒推公式(2)。
这里不想涉及票息和股利处理的技术细节。只要确定票息或股利发放日对应的小时段,在二叉树中相应节点加上票息或除息即可。只是,股利需要采用比例除息方法,避免绝对除息方法带来的路径依赖问题。以下我们重点讨论可转债各种附加条款的处理方法。
附加条款处理
一、提前赎回条款
许多公司发行可转换债券的时候,都附加了可赎回条款,规定当股价超过转换价格的130%情况下,公司有权按预先规定好的价格将发行在外的可转债券赎回,而赎回价格往往定于转换价格附近的水平。一般说来,可赎回条款内容中同时还包括了一个不可赎回期(hard non-call period),规定公司在发行日开始的某一段时期之内无赎回权,常见的不可赎回期为1-3年。
赎回条款在性质上等同于发行者持有的、以其发行在外的可转债券为标的物的美式买权。自然,投资者一旦收到公司的赎回要约,就会在之后一个短暂的缓冲期内执行换股权利,因为没有人会放弃换取溢价至少30%的股票而接受赎回价格。所以,公司拥有的买权实际上绝无实现的时候,其功效只是迫使投资者立即换股。
赎回条款的存在加深了可转债的美式期权性质。可想而知,由于赎回条款赋予公司选择权,而投资者根据当初可转债的寿命作出的较长时段上的期望可能突然落空,可转债价值因此将受到负面影响。
将赎回条款纳入n期二项分布定价模型,首先需要确定公司赎回权利生效的起始时段;以此为界,遴选公司将发出赎回要约的股价区域(以下简称赎回区域),即是说那些股价高于转股价130%的节点;一旦进入赎回区域,相关节点上的可转债价格充其量只可能是当时的股票价格。按照理性原则,发行者将在满足赎回条件的第一时间发出赎回要约。即使公司尚未发出赎回要约,公司强制投资者换股也是预期之中的,没有人会以高于股价S的价格去购买随时可能只值S的可转债。所以,在按照标准的倒推方法得到可转债价值树后,只要将进入赎回区域中第一个节点上可转债的价格调整为股价S,赎回区域以外的可转债价格照常计算,赎回条款就在定价中得到了准确的反映。
二、可回售条款
许多情况下,可转债在发行一段时间以后允许其持有者以预定的价格回售给发行的公司,而预定的回售价格通常(但并不总是)就是其面值。可回售条款相当于以可转债券本身为标的资产的卖权,这份额外的选择权自然会给可转债带来更高的价值。
假定一份可转债合同规定的回售价格为Q,那么在可回售期内任何时候,可转债的价格不可能低于Q。现在只要将这一约束加在原有的n期二项分布定价模型中,即可准确地求出附加回售条款的可转债的价格。基本的方法仍然是从到期日开始向前递推,只是需要利用该约束条件调节相关节点处的可转债估值。具体地讲,在确定二叉树中处于可回售期内一个特定节点处可转债的价值时,先不考虑回售条款,利用倒推基本公式求得该点处可转债的初步估值cb;然后,将这一估值与回售价格比较,取其中较大的一个为该点处的可转债价值:
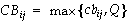
三、向下修正条款
可转债的向下修正条款具体是指:在到期日前某一时刻(称为修正日),若当时的股票市场价格很低,使得将来股价超过原定转换价格的可能性足够小时,将转换价格调整至一个较低的水平--通常情况下,新的转换价会定于当时的股票价格。转换价向下修正条款将可转债的定价过程大大地复杂化了。在二叉树定价模型中,可转债价格只依赖于股票的终值 u d S,但与股票价格二叉树中达到这一终值的路径无关。我们知道,达到股票终值u d S的路径共有n!/k!(n-k)!条,但因为路径无关性,求可转债价格时只需要知道u d S就足够了,这大大简化了计算过程。但是,如果可转债转换价格是可以向下修正的,可转债价格就不再与股价路径无关了,因为在不同的股价路径上,转换价格可能不同。
|
|
解决以上路径依赖问题可以采取两阶段二叉树方法(见图3):
第一阶段,在标准的n期二项式模型中,找到修正日对应的节点,根据修正条款确定这些节点上新的可转债转换价格;以每一个这样的结点为起始点,开始一个二叉“子树”,并根据之前调整过的转换价格,在子树内反推其起始点的可转债价值。这一阶段结束时得到了修正日对应的每一个节点上的可转债价值。
第一阶段,在标准的n期二项式模型中,找到修正日对应的节点,根据修正条款确定这些节点上新的可转债转换价格;以每一个这样的结点为起始点,开始一个二叉“子树”,并根据之前调整过的转换价格,在子树内反推其起始点的可转债价值。这一阶段结束时得到了修正日对应的每一个节点上的可转债价值。
第二阶段,根据上一阶段获得的修正日可转债值,按标准的二叉树反推方法计算最初的可转债价值,完成定价。
四、利率的期限结构问题
无风险利率是任何一种定价方法都必须使用的参数,而二项分布定价模型的另一个灵活性是它能较为合理地融入无风险收益率的期限结构。一种非常普遍的误解是,定价过程应当选用与可转债存续期相同期限的无风险利率(如国债利率)。由于可转债具有美式期权性质,在到期日前存在转股、赎回和回售的可能性,所以我们事前无法确定一张存续期为5年的可转债收益应当以5年、4年甚或是其他期限的无风险利率加以衡量。
换个角度看,由于可转债具有债券和股票二重特征,分别适应长期和短期收益率;而且股价不同,这两种特征的相对强弱程度也不一样。所以,有必要根据股价变化,动态地使用长短期加权的混合利率衡量可转债收益。
我们可以分三种情况考量利率的期限选择问题:
1.如果股价足够低,使得未来根本不存在转股的机会,可转债券将完全等同于单纯债券,应当按照债券定价,所以此时合理的选择是与存续期匹配的长期利率rl。相应地,由于此时可转债价值与股价变化的敏感度为零,可转债的Delta值为零:d=0。
2.在另一个极端,如果股价足够高,到期日转股机会几乎为100%,可将可转债视为等量的股票,而Delta值显然为1。在这情况下,应当选择短期利率rs,衡量投资者的融资成本。
3.在上述两种极端之间,可转债将兼含债券和股票特征,对冲组合受益应当以一个加权平均利率贴现。基于上面对两种极端情况的分析,在一般情况下可以使用下述平均利率:
r=(1-d)rCB+drs (5)
并以其为基础计算可转债价值。
模型在中国市场的应用
同Black-Scholes定价模型一样,二项分布定价模型是基于市场有效假设(EMH)建立的,应用于西方较为成熟的市场来说也许较为贴切,但是对于国内市场来说,其有效性究竟怎样呢?
第一个问题涉及中国上市公司特有的股权结构。由于可转债中的认股权证不完全等同于期权,可转债转股的过程必然导致现有股东每股资产和收益摊薄的稀释效应。但是,自公司刊登可转债发行意向书和正式招募书之后,稀释效应将提前被吸收于当前股价之中,以上定价过程不再需要对稀释率进行调整。从目前拟发行可转债上市公司股票价格的二级市场表现来看,44家上市公司股价在首次公告日后的平均跌幅超过同期大盘跌幅约2%。这可以视为上述论点的一个证据。这样说来,尽管我国上市公司有特殊的所有权结构,在稀释率计算是以总股本还是以流通股本为基数问题上存在较大歧义,但这不影响我们模型定价的过程和结果。
另一方面,上述模型最根本的基础是市场有效性假设(EMH)。最起码,它要求可转债与标的股票所处的市场环境至少是相似的。但是,中国股票市场充其量只是勉强满足弱式的EMH ,而且最大的现实问题在于,股票和可转债交易处于完全不同的两个市场环境,而这两个市场环境内资金供给量等影响交易价格的因素有很大的区别。
目前,我国股票市场已具有相当规模,深沪两市交易的上市公司股票有1000多只,而挂牌交易的可转债只有机场转债、鞍钢转债和茂炼转债三家;从成交量来说,上海和深圳市场每日股票成交金额最少也有几十亿人民币,但3只可转债每日成交金额通常只有区区几十万元,可转债缺乏流动性问题十分突出。由于成交量极小,价格对买单数额变化非常敏感,造成可转债市场对基金等机构投资者的吸引力相当微弱。
从股票和可转债的价格规律来看,股票价格从理论上讲不存在上下限--通过控制买卖数量,“庄家”可以将一只股票的价格任意拉抬或打压;相形之下,可转债价格却受标的股票价格的牵制--在标的股票价格不变的情况下,可转债价格值可能在一个相当狭小的箱形区域内运动(由于套利规律作用)。这意味着,除非先操纵标的股票的价格,任何人无法大幅度地拉升或打压可转债价格。
这些因素的存在会对模型定价结果产生什么样的影响?显然,如果标的股票的价格中存在人为因素,可转债定价模型给出的结果必然会与实际观察值有相当的偏差。事实上,我们认为在国内证券市场的现状下理论模型通常会高估可转债的价值。理由在于:
第一,由于流通性较强,价格变动约束较小,股票市场能吸引更多的机构投资者和大户,资金供给较为充裕;相反,可转债市场严重缺乏流通性,投资者主流是散户,资金供给较为紧张。
第二,由于部分机构投资者和大户的刻意拉抬,不少股票价格水分严重;并且由于示范效应,即使不是庄股,其价格也容易出现高估现象。相反,可转债市场不仅不存在庄家拉抬价格的环境,而且非常低的交易量也不支持价格走高。
第三,可转债模型定价所需的一个主要参数是标的股票预期的收益波动率,而根据国内股票发展的状况,目前我们对股票收益波动率的估计很容易过高。对未来股票价格波动率的估计,最主要的根据是股票的历史价格。但是在此之前,中国股票市场庄家操纵价格的现象比较普遍,其主要表现之一是股价在短时间内暴涨或暴跌,这会给出大多数股票较高的股价波动率估计。但是,今年以来政府明显加强了市场监管,而且随着市场的发展,相信未来市场将在更为规范的轨道上运行。在系统性的股价波动率有长期下降趋势的情况下,可转债价格也会被模型高估。
由于上述原因,二项分布定价模型应用于中国市场的时候,理论估价往往会比实际市场价格高,但这并不一定意味着市场低估了可转债价值,具体情况还需根据可转债发行者行业特征、经营状况等基本面情况进行进一步修正。
举例来说,按上述二项分布模型,2001年10月19日上海证券交易所上市的机场转债(见表1)价值当为106.71元,但当日的实际收盘价格却是97.96元,低于理论值8.20%。这是否意味着当日上海机场股票7.97元的收盘价含有泡沫呢?维持模型参数不变,我们从转债的实际价格对股票价格作了反推,结果表明与机场转债实际价格97.96元相吻合的上海机场股票价格是3.06元!如果说从各个方面考虑这都不是投资者可以接受的价位(注意,近期上海机场股价已有超过20%的跌幅),可以认为机场转债理论价格的相对高估至少不完全是由股价过高引起的。另一方面,与97.96元相匹配的股价波动率倒推值是8.21%(其他模型参数不变),这也与直觉上的上海机场股票预期波动率相去甚远。基于这两方面的分析,我们认为机场转债的价值的确被市场低估了(虽然低估的幅度可能小于8.20%),而造成这种扭曲的原因就是目前可转债市场规模过小造成的流动性严重缺乏。
这个例子说明,也许只有当上市交易的可转债品种增加到一定数量,市场发展到一定规模,能吸引更多的机构投资者进入,使得股市和债市的市场环境差距缩小,并且整个证券市场的运作和监管都进一步规范化之后,对可转债进行准确定价才有可能。 ■